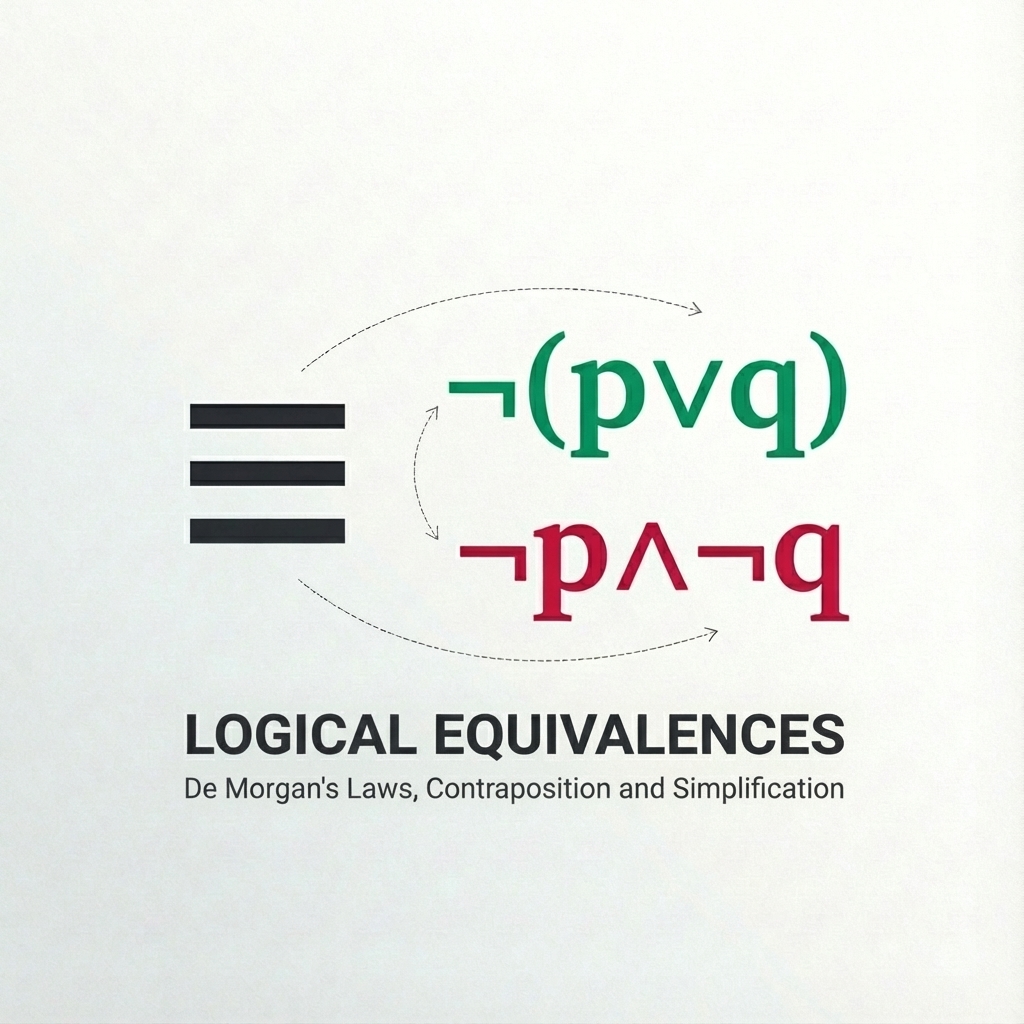Tabla de contenido
In this lesson, you’ll learn how to simplify complex logical expressions using established rules. In this guide, you’ll use the laws of logical equivalence, fundamental tools for transforming and simplifying propositions without changing their truth value.
What is a Logical Equivalence?
Two propositions are logically equivalent when they have exactly the same truth values for all possible combinations of their variables.
Formal Definition
We say that p ≡ q (p is equivalent to q) if and only if p ↔ q is a tautology.
In other words, p and q are equivalent when the biconditional between them is always true.
Equivalence Symbols
| Symbol | Usage |
|---|---|
| ≡ | Logical equivalence (most common) |
| ⇔ | Some textbooks |
| ⟺ | Alternative notation |
What are equivalences used for?
The laws of equivalence allow you to:
- Simplify complex logical expressions
- Prove that two expressions are equal without using truth tables
- Transform an expression into a more convenient form
- Verify logical arguments
Fundamental Laws of Equivalence
1. Identity Law
A proposition combined with certain constant values maintains its identity (remains the same proposition):
| Law | Formula | Explanation |
|---|---|---|
| Identity with T | p ∧ T ≡ p | “p AND true” is simply p |
| Identity with F | p ∨ F ≡ p | “p OR false” is simply p |
Example:
- “Today is Monday AND it’s true that 2+2=4” ≡ “Today is Monday”
- “It’s raining OR it’s false that pigs fly” ≡ “It’s raining”
2. Domination Law (Absorbing Element)
Certain constant values dominate or absorb the proposition, making the result solely that constant value (the proposition “disappears”):
| Law | Formula | Explanation |
|---|---|---|
| Domination with T | p ∨ T ≡ T | “p OR true” is always true |
| Domination with F | p ∧ F ≡ F | “p AND false” is always false |
Example:
- “I’m a millionaire OR 2+2=4” ≡ T (always true)
- “I’m a millionaire AND 2+2=5” ≡ F (always false)
3. Idempotent Law
A proposition repeated with the same connective gives the same proposition:
| Law | Formula |
|---|---|
| Idempotence of ∧ | p ∧ p ≡ p |
| Idempotence of ∨ | p ∨ p ≡ p |
Example:
- “It’s raining AND it’s raining” ≡ “It’s raining”
- “It’s cold OR it’s cold” ≡ “It’s cold”
4. Double Negation Law
Negating a proposition twice returns it to its original state:
| Law | Formula |
|---|---|
| Double Negation | ¬(¬p) ≡ p |
Example:
- “It’s not false that it’s raining” ≡ “It’s raining”
- “It’s not true that I didn’t pass” ≡ “I passed”
5. Complement Law (Excluded Middle and Contradiction)
| Law | Formula | Name |
|---|---|---|
| p ∨ ¬p ≡ T | Excluded Middle | A proposition or its negation is true |
| p ∧ ¬p ≡ F | Contradiction | A proposition cannot be T and F at the same time |
Example:
- “Today is Monday OR today is not Monday” ≡ T (always true)
- “Today is Monday AND today is not Monday” ≡ F (always false)
Laws of Operations Between Propositions
6. Commutative Law
The order of propositions does not affect the result:
| Law | Formula |
|---|---|
| Commutativity of ∧ | p ∧ q ≡ q ∧ p |
| Commutativity of ∨ | p ∨ q ≡ q ∨ p |
| Commutativity of ↔ | p ↔ q ≡ q ↔ p |
Example:
- “It’s raining AND it’s cold” ≡ “It’s cold AND it’s raining”
- “John is tall OR Peter is short” ≡ “Peter is short OR John is tall”
Note: The conditional (→) is NOT commutative. “If it rains, I get wet” is NOT equivalent to “If I get wet, it rains.”
7. Associative Law
The grouping of propositions does not affect the result:
| Law | Formula |
|---|---|
| Associativity of ∧ | (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) |
| Associativity of ∨ | (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) |
Example:
- “(A AND B) AND C” ≡ “A AND (B AND C)”
- We can simply write: A ∧ B ∧ C
8. Distributive Law
One connective can be “distributed” over another:
| Law | Formula |
|---|---|
| ∧ distributes over ∨ | p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) |
| ∨ distributes over ∧ | p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) |
Example:
- “I study AND (I pass OR I fail)” ≡ “(I study AND I pass) OR (I study AND I fail)”
Analogy with algebra: Similar to a × (b + c) = ab + ac
9. Absorption Law
A proposition “absorbs” another when they are connected in a certain way:
| Law | Formula |
|---|---|
| Absorption 1 | p ∧ (p ∨ q) ≡ p |
| Absorption 2 | p ∨ (p ∧ q) ≡ p |
Example:
- “It’s raining AND (it’s raining OR it’s sunny)” ≡ “It’s raining”
- “John passes OR (John passes AND studies)” ≡ “John passes”
Explanation:
- In the first case: if p is T, the whole expression is T (because of p). If p is F, (p ∨ q) could be T, but p ∧ (something) would be F.
- In both cases, the result matches p.
De Morgan’s Laws
De Morgan’s Laws are perhaps the most important and useful in logic. They allow you to “pass” a negation through a conjunction or disjunction.
Formulation
| Law | Formula | In words |
|---|---|---|
| De Morgan 1 | \( \neg ( \mathrm{p} ∧ \mathrm{q} ) ≡ \neg \mathrm{p} ∨ \neg \mathrm{q} \) | “NOT (p AND q)” equals “NOT p OR NOT q” |
| De Morgan 2 | \( \neg (\mathrm{p} ∨ \mathrm{q} ) ≡ \neg \mathrm{p} ∧ \neg \mathrm{q} \) | “NOT (p OR q)” equals “NOT p AND NOT q” |
Mnemonic Rule
When negating an expression: change ∧ to ∨ (and vice versa) and negate each component.
Detailed Examples
Example 1: Negate “It’s raining AND it’s cold”
- ¬(Raining ∧ Cold)
- ≡ ¬Raining ∨ ¬Cold
- = “It’s not raining OR it’s not cold”
Example 2: Negate “John is a student OR is a worker”
- ¬(Student ∨ Worker)
- ≡ ¬Student ∧ ¬Worker
- = “John is not a student AND is not a worker”
Example 3: In programming
In languages like JavaScript, Java, or C, logical operators are written differently:
| Logic | Programming | Meaning |
|---|---|---|
| ¬ | ! | Negation (NOT) |
| ∧ | && | Conjunction (AND) |
| ∨ | ` |
Applying De Morgan, these two conditions are equivalent:
// Form 1: Negate the entire conjunction
if (!(x > 5 && y < 10)) { ... }
// Form 2: Negate each part and change && to ||
if (x <= 5 || y >= 10) { ... }
Explanation:
!(x > 5)becomesx <= 5(negating “greater than” is “less than or equal”)!(y < 10)becomesy >= 10(negating “less than” is “greater than or equal”)- The
&&(AND) becomes||(OR)
Extended Application
De Morgan’s Laws also apply to multiple propositions:
| Expression | Equivalent |
|---|---|
| ¬(p ∧ q ∧ r) | ¬p ∨ ¬q ∨ ¬r |
| ¬(p ∨ q ∨ r) | ¬p ∧ ¬q ∧ ¬r |
Conditional Equivalences
The conditional (→) has several very important equivalent forms.
10. Material Implication
The conditional can be expressed using only negation and disjunction:
| Law | Formula |
|---|---|
| Material Implication | p → q ≡ ¬p ∨ q |
Interpretation: “If p then q” is the same as “Not p, OR q”
Example:
- “If it rains, I get wet” ≡ “It doesn’t rain OR I get wet”
- “If you study, you pass” ≡ “You don’t study OR you pass”
11. Contraposition Law (Contrapositive)
The conditional is equivalent to its contrapositive:
| Law | Formula |
|---|---|
| Contraposition | p → q ≡ ¬q → ¬p |
Example:
- “If it rains, the street gets wet” ≡ “If the street is NOT wet, it’s NOT raining”
- “If you’re a mammal, you’re a vertebrate” ≡ “If you’re NOT a vertebrate, you’re NOT a mammal”
Important: The contrapositive always has the same truth value as the original proposition. This is very useful in mathematical proofs.
12. Negation of the Conditional
To negate a conditional, affirm the antecedent and negate the consequent:
| Law | Formula |
|---|---|
| Conditional Negation | ¬(p → q) ≡ p ∧ ¬q |
Example:
- Negate “If you study, you pass”
- ≡ “You study AND you do NOT pass”
Explanation: The only case where p → q is FALSE is when p is T and q is F.
13. Other Conditional Equivalences
| Equivalence | Formula |
|---|---|
| Using negation | p → q ≡ ¬(p ∧ ¬q) |
| Multiple transposition | p → q ≡ ¬q → ¬p ≡ ¬(p ∧ ¬q) ≡ ¬p ∨ q |
Biconditional Equivalences
14. Definition as Double Conditional
The biconditional is the conjunction of two opposite conditionals:
| Law | Formula |
|---|---|
| Biconditional | p ↔ q ≡ (p → q) ∧ (q → p) |
Interpretation: “p if and only if q” means “If p then q” AND “If q then p”
15. Alternative Form
The biconditional can also be expressed as:
| Law | Formula |
|---|---|
| Biconditional (alt) | p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q) |
Interpretation: “p ↔ q” is true when “both are true OR both are false”
16. Negation of the Biconditional
| Law | Formula |
|---|---|
| Negation ↔ | ¬(p ↔ q) ≡ p ⊻ q |
The negation of the biconditional is the exclusive disjunction (XOR).
17. Equivalence of Negations
| Law | Formula |
|---|---|
| Equivalent negations | p ↔ q ≡ ¬p ↔ ¬q |
Example: “You pass if and only if you score 60%” ≡ “You don’t pass if and only if you don’t score 60%”
18. Exportation Law
This law relates nested conjunctions with conditionals:
| Law | Formula |
|---|---|
| Exportation | (p ∧ q) → r ≡ p → (q → r) |
Example:
- “If (you study AND practice), you pass” ≡ “If you study, then (if you practice, you pass)”
Equivalence Summary Table
| Name | Formula |
|---|---|
| 1. Identity | p ∧ T ≡ p p ∨ F ≡ p |
| 2. Domination | p ∨ T ≡ T p ∧ F ≡ F |
| 3. Idempotence | p ∧ p ≡ p p ∨ p ≡ p |
| 4. Double Negation | ¬(¬p) ≡ p |
| 5. Complement | p ∨ ¬p ≡ T p ∧ ¬p ≡ F |
| 6. Commutativity | p ∧ q ≡ q ∧ p p ∨ q ≡ q ∨ p |
| 7. Associativity | (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) |
| 8. Distributivity | \( \mathrm{p} ∧ ( \mathrm{q} ∨ \mathrm{r} ) ≡ ( \mathrm{p} ∧ \mathrm{q} ) ∨ ( \mathrm{p} ∧ \mathrm{r} ) \) |
| 9. Absorption | p ∧ (p ∨ q) ≡ p p ∨ (p ∧ q) ≡ p |
| 10. De Morgan | ¬(p ∧ q) ≡ ¬p ∨ ¬q ¬(p ∨ q) ≡ ¬p ∧ ¬q |
| 11. Material Implication | p → q ≡ ¬p ∨ q |
| 12. Contraposition | p → q ≡ ¬q → ¬p |
| 13. Conditional Negation | ¬(p → q) ≡ p ∧ ¬q |
| 14. Biconditional | p ↔ q ≡ (p → q) ∧ (q → p) |
| 15. Biconditional (alt) | p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q) |
| 16. Biconditional Negation | ¬(p ↔ q) ≡ p ⊻ q |
| 17. Negation Equivalence | p ↔ q ≡ ¬p ↔ ¬q |
| 18. Exportation | (p ∧ q) → r ≡ p → (q → r) |
Application: Simplifying Expressions
Example 1: Simplify:
¬(p ∨ ¬q)
- Apply De Morgan: ¬p ∧ ¬(¬q)
- Apply Double Negation: ¬p ∧ q
Result: ¬(p ∨ ¬q) ≡ ¬p ∧ q
Example 2: Simplify:
(p ∧ q) ∨ (p ∧ ¬q)
- Factor out common term (reverse Distributive): p ∧ (q ∨ ¬q)
- Apply Excluded Middle: p ∧ T
- Apply Identity: p
Result: (p ∧ q) ∨ (p ∧ ¬q) ≡ p
Example 3: Prove that:
p → q ≡ ¬q → ¬p
| Step | Expression | Law applied |
|---|---|---|
| 1 | p → q | Initial expression |
| 2 | ¬p ∨ q | Material Implication |
| 3 | q ∨ ¬p | Commutativity |
| 4 | ¬(¬q) ∨ ¬p | Double Negation |
| 5 | ¬q → ¬p | Material Implication (reverse) |
Practice Exercises
Exercise 1: Simplification
Simplify the following expressions using the laws of equivalence:
- p ∧ (p ∨ q)
- ¬(¬p ∧ ¬q)
- (p → q) ∧ (p → ¬q)
- p ∨ (¬p ∧ q)
Exercise 2: Proof
Prove the following equivalences step by step:
- ¬(p → q) ≡ p ∧ ¬q
- p → (q → r) ≡ (p ∧ q) → r
- p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q)
Exercise 3: Negation
Negate the following propositions and simplify:
- “If it rains, then it’s cold AND there are clouds”
- “You pass if and only if you study”
- “It’s not true that (p OR q)”
Answers
Answers to Exercise 1
- p ∧ (p ∨ q) ≡ p (Absorption)
- ¬(¬p ∧ ¬q) ≡ p ∨ q (De Morgan)
- (p → q) ∧ (p → ¬q):
- ≡ (¬p ∨ q) ∧ (¬p ∨ ¬q) (Material Implication)
- ≡ ¬p ∨ (q ∧ ¬q) (Distributive)
- ≡ ¬p ∨ F (Contradiction)
- ≡ ¬p (Identity)
- p ∨ (¬p ∧ q):
- ≡ (p ∨ ¬p) ∧ (p ∨ q) (Distributive)
- ≡ T ∧ (p ∨ q) (Excluded Middle)
- ≡ p ∨ q (Identity)
Answers to Exercise 2
- ¬(p → q) ≡ p ∧ ¬q:
- ¬(p → q)
- ≡ ¬(¬p ∨ q) (Material Implication)
- ≡ ¬(¬p) ∧ ¬q (De Morgan)
- ≡ p ∧ ¬q (Double Negation) ✓
- p → (q → r) ≡ (p ∧ q) → r:
- p → (q → r)
- ≡ p → (¬q ∨ r) (Material Implication)
- ≡ ¬p ∨ (¬q ∨ r) (Material Implication)
- ≡ (¬p ∨ ¬q) ∨ r (Associativity)
- ≡ ¬(p ∧ q) ∨ r (De Morgan)
- ≡ (p ∧ q) → r (Material Implication) ✓
- p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q):
- p ↔ q
- ≡ (p → q) ∧ (q → p) (Biconditional Definition)
- ≡ (¬p ∨ q) ∧ (¬q ∨ p) (Material Implication, twice)
- ≡ [(¬p ∨ q) ∧ ¬q] ∨ [(¬p ∨ q) ∧ p] (Distributive)
- ≡ [(¬p ∧ ¬q) ∨ (q ∧ ¬q)] ∨ [(¬p ∧ p) ∨ (q ∧ p)] (Distributive)
- ≡ [(¬p ∧ ¬q) ∨ F] ∨ [F ∨ (p ∧ q)] (Contradiction)
- ≡ (¬p ∧ ¬q) ∨ (p ∧ q) (Identity)
- ≡ (p ∧ q) ∨ (¬p ∧ ¬q) (Commutativity) ✓
Answers to Exercise 3
- Negate “If it rains, then (it’s cold AND there are clouds)”:
- ¬(Rains → (Cold ∧ Clouds))
- ≡ Rains ∧ ¬(Cold ∧ Clouds)
- ≡ Rains ∧ (¬Cold ∨ ¬Clouds)
- = “It rains AND (it’s not cold OR there are no clouds)”
- Negate “You pass if and only if you study”:
- ¬(Pass ↔ Study)
- ≡ Pass ⊻ Study
- = “You pass OR you study, but not both” (XOR)
- Negate “It’s not true that (p OR q)”:
- ¬(¬(p ∨ q))
- ≡ p ∨ q (Double Negation)
What’s Next?
In the next article, we’ll study what logical inference is, its notable laws, and the abbreviated method.
Did you find this post useful? Leave me a comment with your questions or suggestions! And don’t forget to check out the next installment of this series on mathematical logic.